初心者でもわかる二分探索法：簡単な実装とその優れた効率性

2024年12月25日 21:03

二分探索法は、各反復で探索範囲を半分に分割する探索アルゴリズムです。目的の値との比較に基づいて半分を破棄し、残りの半分で目的の値が見つかるか、探索範囲が空になるまで探索を続けます。
二分探索法を適用するには、データの集合が昇順または降順にソートされている必要があります。このアルゴリズムは各反復で探索範囲を半分に減らすため、目的の値を見つけるために必要な比較回数が大幅に削減されます。

なぜ二分探索法を使用するのか？

二分探索法は、ソートされた大規模なデータ集合に対して非常に効率的なアルゴリズムです。時間計算量はO(log n)であり、これはn個の要素を持つ集合から要素を探索するのに必要な時間がlog nに比例することを意味します。これは、時間計算量がO(n)である線形探索よりもはるかに高速です。

二分探索法の実装

二分探索法は再帰的または反復的に実装できます。どちらの方法でも、まずデータがソートされていることを確認する必要があります。

再帰を用いた二分探索法

const binarySearchRecursive = (arr, target, start = 0, end = arr.length - 1) => {
  if (start > end) {
  // target not found
    return -1; 
  }
  
  const mid = Math.floor((start + end) / 2);
  
  if (arr[mid] === target) {
  // target found
    return mid; 
  }
  
  if (target < arr[mid]) {
  // search in the left half
    return binarySearchRecursive(arr, target, start, mid - 1);
  } else {
  // search in the right half
    return binarySearchRecursive(arr, target, mid + 1, end);
  }
}

配列、目的の値、探索範囲の開始インデックスと終了インデックスを入力として受け取ります。
開始インデックスが終了インデックスより大きい場合、目的の値が見つからなかったことを示す-1を返します。そうでない場合、中間インデックス(start + end) / 2を計算し、この位置の値と目的の値を比較します。Math.floor()は、結果が小数の場合に切り捨てを行います。例えば9.5は9に切り捨てられます。
値が等しい場合は中間インデックスを返します。そうでない場合、比較結果に基づいて半分を破棄し、残りの半分で探索を続けます。
この過程を目的の値が見つかるか、探索範囲が空になるまで繰り返します。

反復を用いた二分探索法

const binarySearchIterative = (arr, target) => {
  let start = 0;
  let end = arr.length - 1;
  
  while (start <= end) {
    const mid = Math.floor((start + end) / 2);
    
    if (arr[mid] === target) {
    // target found
      return mid;
    }
    
    if (target < arr[mid]) {
    // search in the left half
      end = mid - 1;
    } else {
    // search in the right half
      start = mid + 1; 
    }
  }
  
  // target not found
  return -1;
}

配列全体を初期の探索範囲とします。
開始インデックスが終了インデックスより大きくなるまで（目的の値が見つからないことを示す）、while ループで探索を続けます。
各反復で、探索範囲の中間インデックス(start + end) / 2を計算し、この位置の値と目的の値を比較します。
値が等しい場合は中間インデックスを返します。そうでない場合、半分を破棄し、開始インデックスと終了インデックスを適切に更新します。
この過程を目的の値が見つかるか、探索範囲が空になるまで繰り返します。

百聞は一見に如かずと言いますが。

以下のアニメーションでは、二分探索法の仕組みを視覚的に明確に示しています。長い説明で概念を理解しようと苦労するのではなく、このアニメーションによって二分探索法の動作メカニズムを直感的かつ効率的に把握することができます。

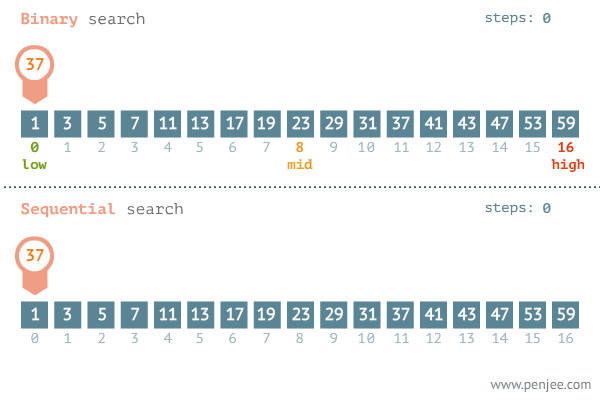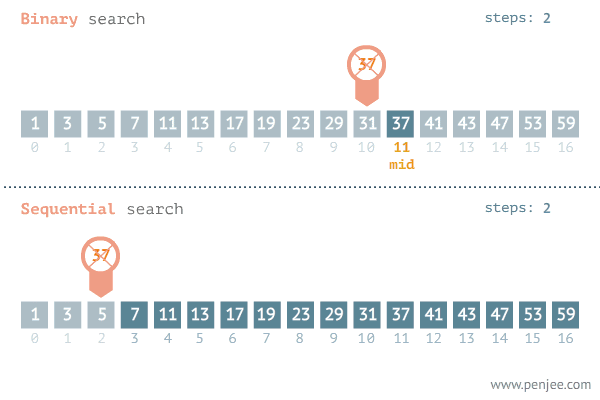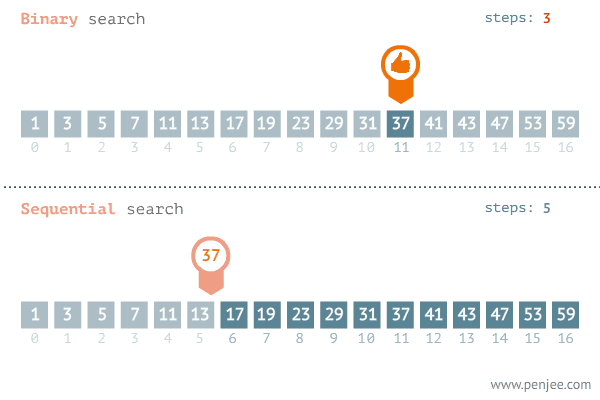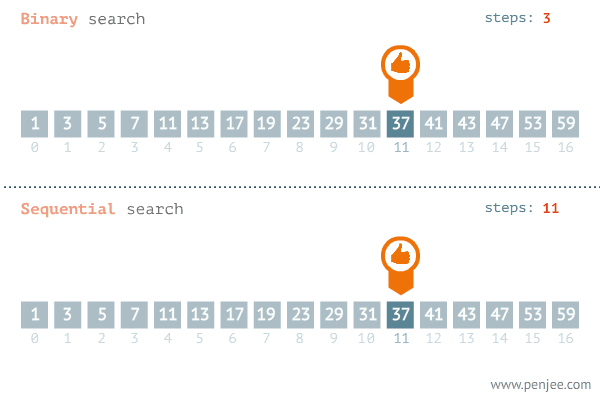
二分探索法の計算量分析

二分探索法の時間計算量を分析するには、目的の値を見つけるために必要な比較回数を考慮する必要があります。各反復で探索範囲が半分になるため、時間計算量はO(log n)となります。これは、n個の要素を持つ集合から要素を探索するのに必要な時間がlog nに比例することを意味します。
空間計算量に関しては、反復的な実装ではO(1)、再帰的な実装ではO(log n)となります。再帰的な実装では、再帰呼び出しを格納するためにコールスタックを使用するため、空間計算量はO(log n)となります。

まとめ

二分探索法の基礎を理解できましたね！覚えておくべき重要なポイントは、二分探索法は大規模なデータセットを扱う際に真価を発揮するということです。小規模なデータセットの場合、for ループのような単純なアルゴリズムの方が二分探索法と同等かそれ以上に効率的な場合があります。

この記事は、2023 年 5 月に弊社エンジニアの Raju Shrestha が執筆し、日本語に翻訳したものです。
英語版はこちらをクリックしてください。
https://articles.wesionary.team/implementing-binary-search-a-simple-guide-3aa89453e0d2

採用情報

私たちはプロダクト共創の仕組み化に取り組んでいます。プロダクト共創をリードするプロダクト・マネージャー、そして、私たちのビジョンを市場に届ける営業メンバーを募集しています！

開発パートナーをお探しの企業様へ

弊社は、グローバル開発のメリットを活かし、高い費用対効果と品質を両立しています。経験豊富で多様性のあるチームが、課題を正しく理解し、最適なシステムと優れた体験を実現します。業務システムの開発、新規事業の開発、業務効率化やDX化に関するお困りごと、ぜひ弊社にご相談ください。